
- By Javier Martínez
- ·
- Posted 10 Aug 2021
Functional patterns
Welcome pythonistas! In our last video session on design patterns we focused exclusively on patterns for the object oriented paradigm (OOP). To some..
In the previous posts we stated that functional programs should limit side effects. If we take that hypothesis as true, how can we implement a List? At a first glance, a data structure to hold data seems the opposite to avoid side effects. In this post, we will see how to implement a List in Scala and how to use it. Please notice that other programming languages could be used as well and some of them use the same approach in their List implementations.
Lists are recursive data structures, that is structures which one of its nodes refers to itself, you will see that in a minute. They could be formed by two different types of nodes, an empty node or a node with one element followed by another node. In Scala the constructor for the empty node is called Nil and the constructor for the node which has the element and the following node is called ::. In :: we call head the element contained in the node and tail to the following node.
A pseudocode representation of a List could be:
List = (head followed by List) or EndOfListNotice the recursive nature of this definition: the List contains another List inside
The Scala representation for List is:
sealed trait List[+A]
case class ::[+A](head: A, tail: List[A]) extends List[A]
case object Nil extends List[Nothing]
:: represents the statement that we made before, a List is just a head element followed by another List. Nil is just a representation of an empty List, it could be called EOL (End of List) as well.
In scala we can construct a List with the elements 1, 2 and 3 using the function apply:
List(1, 2, 3)
Which is a shorthand to write this:
1 :: 2 :: 3 :: Nil
Where :: is the constructor that we defined before but used as an infix. We can construct it without the infix notation like this:
::(1, ::(2, ::(3, Nil)))
In that last representation, we can see exactly how the structure is constructed without the infix notation. That makes us notice that a list is not flat but instead it has a concept of nesting elements to form longer lists. No one creates a List like that, but is easier to see the head and tail concepts in that representation. Also, we can see that the structure is left associative, meaning that the parenthesis to construct the structure are aligned to the left.
We can even represent this construction as a tree:
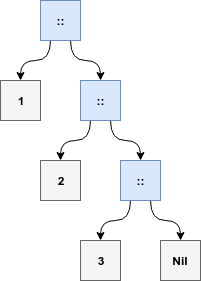
The blue boxes are the recursive nodes that construct the structure, we call that blue boxes the spine of the data structure.
When we talk about persistence in relation with a data structure we don’t refer to anything related to store that data structure on a DB or anything similar. A data structure is persistent when the different versions of it are available at the same time. Said in another manner: we create a new structure every time we would like to modify something. These data structures are immutable given that the contents of them can't be modified.
If we have an empty list and we need to add an element we will have both versions of the list, the first one: List() and the second version with element append: List(element). We can prove this with this piece of code:
@ val initialList = List()
initialList: List[Nothing] = List()
@ val listPlusOne = initialList ++ List(1)
listPlusOne: List[Int] = List(1)
@ println(initialList)
List()
As you can see initialList is still available and hasn't mutated its value.
We can classify persistence in two categories:
So, is List a fully persistent structure or is it only partial? Let's try to figure out trying to modify twice the same structure:
@ val initialList = List(1)
initialList: List[Int] = List(1)
@ val firstVersion = initialList ++ List(2)
firstVersion: List[Int] = List(1, 2)
@ val initialListAppendedNode = initialList ++ List(3)
initialListAppendedNode: List[Int] = List(1, 3)
You bet! Is fully persistent. In that piece of code, you can see how we can append elements to the initial list even if we created other versions.
If you are wondering what could be a partially persistent structure you can think about a balanced binary search tree. After an insert operation you are forced to use the last version of the structure to continue adding nodes given that this structure performs some balancing at the nodes. You can read more here, at page 92 But this is out of scope for this post.
Maybe you are wondering if creating different versions of the same List is expensive memory-wise. Well, we are creating a new structure but the nodes and values are pointers to the same cells in memory. Using immutability we know that those values are not going to be modified, so we can reference them from different structures safely.
If we append two lists we will end up with a new list with the results of concatenating both. Remember that the objects inside the list will remain the same, let's see this visual representation as an example:
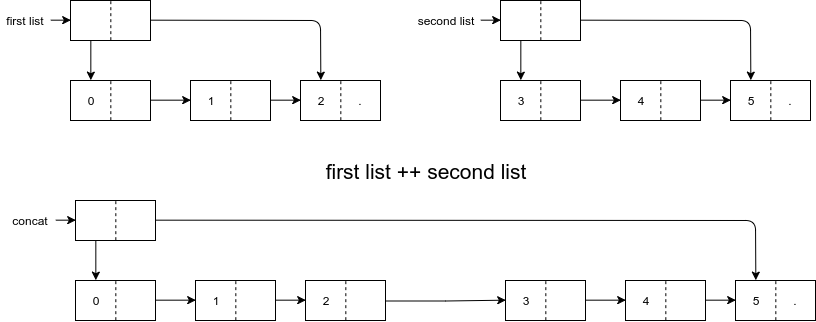
Tails are pointers to other structures that we have in memory so inserting elements is just a matter of linking that pointer together. That allows us to have different versions of the List in memory at the same time without fully consuming the memory of the computer.

Welcome pythonistas! In our last video session on design patterns we focused exclusively on patterns for the object oriented paradigm (OOP). To some..

Solving a simple problem in Elixir In this article, I am going to solve the Word Count problem from Exercism in Elixir. I'll start with a form that..
Crafting web apps using finite state machines - Part 1 Code on Gitlab
Join our newsletter for expert tips and inspirational case studies
Join our newsletter for expert tips and inspirational case studies